Identify the cathode and anode, write the net cell equation, and calculate the cell potential for #"Pt"(s) | "SO"_4^(2-)(aq), "H"^(+)(aq) | "H"_2"SO"_3(aq) "||" "Ag"^(+)(aq) | "Ag"(s)#?
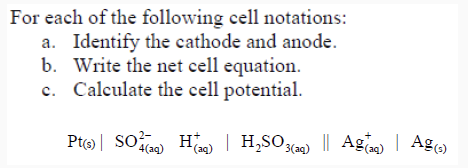
1 Answer
There's a small trick here... Ignoring the charge balance, the main action going on in one half-reaction is:
#"SO"_4^(2-)(aq) -> "H"_2"SO"_3(aq) -> "H"_2"O"(l) + "SO"_2(g)#
As a result, we find the two half-reactions to be:
#"Ag"^(+)(aq) + e^(-) -> "Ag"(s)# ,#E_(red)^@ = +"0.80 V"#
#"SO"_4^(2-)(aq) + 4"H"^(+)(aq) + 2e^(-) -> "SO"_2(g) + 2"H"_2"O"(l)# ,#E_(red)^@ = +"0.20 V"#
The silver reduction has a more positive
Thus, we reverse the other half-reaction to write it as an oxidation and the decomposition of sulfurous acid leads to the oxidation of sulfur dioxide to sulfate at the anode.
#E_(o x)^@(2) = -E_(red)^@ (2) = -(+"0.20 V") = -"0.20 V"#
The reactions add up as:
#2("Ag"^(+)(aq) + cancel(e^(-)) -> "Ag"(s))#
#ul(stackrel(color(blue)(+4))("S")"O"_2(g) + 2"H"_2"O"(l) -> stackrel(color(blue)(+6))("S")"O"_4^(2-)(aq) + 4"H"^(+)(aq) + cancel(2e^(-)))#
#color(blue)(2"Ag"^(+)(aq) + "SO"_2(g) + 2"H"_2"O"(l) -> 2"Ag"(s) + "SO"_4^(2-)(aq) + 4"H"^(+)(aq))#
For this reaction, we then get:
#color(blue)(E_(cell)^@) = E_(red)^@ + E_(o x)^@#
#= "0.80 V" + (-"0.20 V") = color(blue)(+"0.60 V")#
And we do not multiply

