why [CuCl4]2- has a flattened tetrahedral structure, not regular tetrahedron and [CoCl4]2- is tetrahedron?

It's probably a Jahn-Teller distortion.

From the electron configuration of the atoms:

#"Cu": [Ar] 3d^10 4s^1#
#"Co": [Ar] 3d^7 4s^2#

Take away two electrons and you have the #+2# oxidation states for both:

#"Cu"^(2+): [Ar] 3d^9 4s^0#
#"Co"^(2+): [Ar] 3d^7 4s^0#

Therefore, we have a #d^9# complex in #["CuCl"_4]^(2-)#, and a #d^7# complex in #["CoCl"_4]^(2-)#.

Their ORIGINAL tetrahedral d-orbital splitting diagrams would look like:

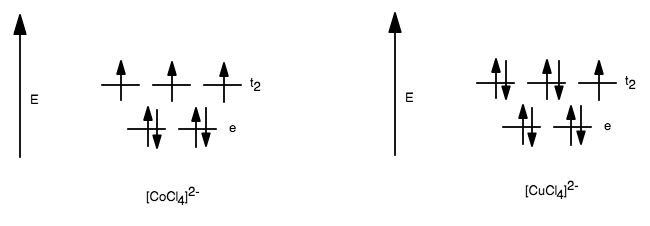
But we can see that there are multiple ways to fill the orbitals in #"CuCl"_4^(2-)# and still get the same number of electrons in each orbital.

Three ways, actually, because the #t_2# orbitals are triply degenerate.

#ul(uarr darr)" "ul(uarr darr)" "ul(uarr color(white)(darr))# #" "bb((1))#

#ul(uarr darr)" "ul(uarr color(white)(darr))" "ul(uarr darr)# #" "bb((2))#

#ul(uarr color(white)(darr))" "ul(uarr darr)" "ul(uarr darr)# #" "bb((3))#

Therefore, to relieve this degeneracy (at least somewhat), a Jahn-Teller distortion occurs to descend in symmetry from tetrahedral #T_d# to trigonal pyramidal #C_(3v)#.

[This is analogous to the Jahn-Teller distortion that forces the octahedral #O_h# symmetry to descend to square bipyramidal #D_(4h)#.]

Here is how each irreducible representation correlates:

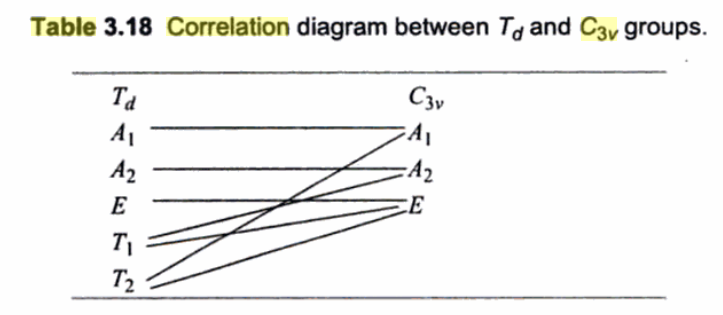
We have:

#E -> E#

#T_2 -> A_1 + E#

The orbitals will therefore split in energy as follows:

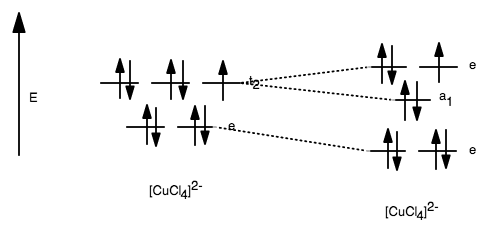
As it turns out, this is not going to completely lift the degeneracy. There is still a double degeneracy in the #e# orbitals highest in energy.

The transition metal complex distorts as follows:

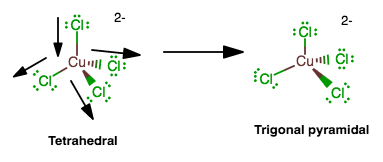
and if the bonds stretch in the other direction, the orbitals will be in order of energy as #e, e, a_1# instead of #e,a_1,e#.