Why change in dipole moment or fluctuating dipole moment is necessary for absorption of infrared radiation?

Molecular Polarity

Let's use a simple molecule like #"HCl"# as an example.

It is a polar molecule because there is a separation of charge that gives the molecule a dipole moment.

Thus, the molecules align themselves with an electric field, as in the diagram below.

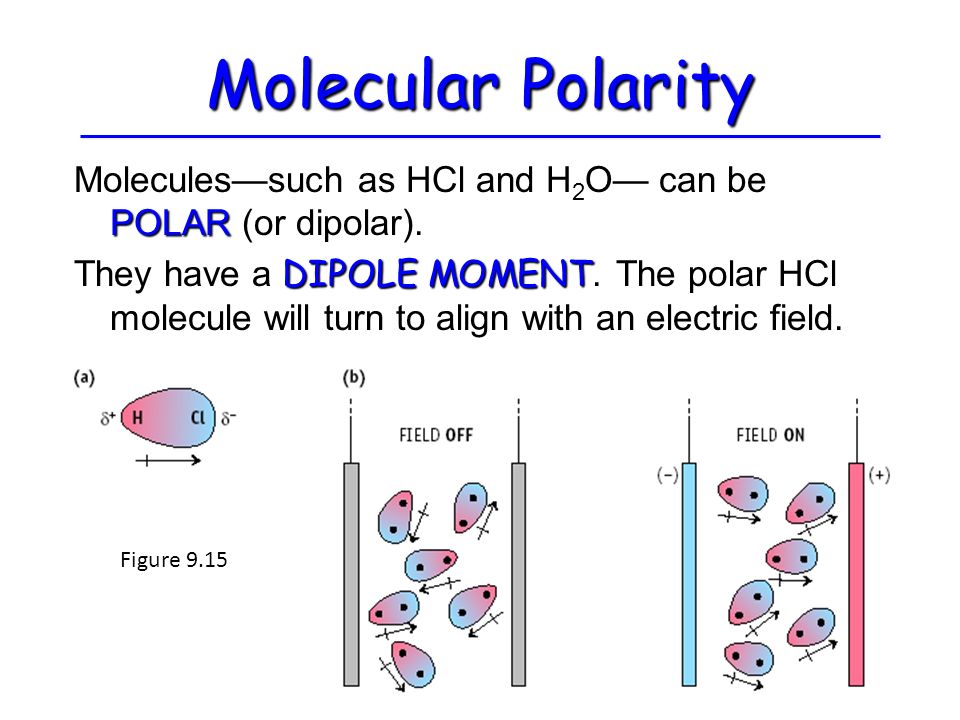
If the charge on the plates is reversed, the molecules will reverse their orientation to point in the opposite direction.

If the charge oscillates back and forth, the molecules will also oscillate back and forth.

Oscillating dipole

The dipole in a molecule is not static.

As the bond vibrates, the distance between the charges increases and decreases, so the dipole moment also oscillates back and forth.

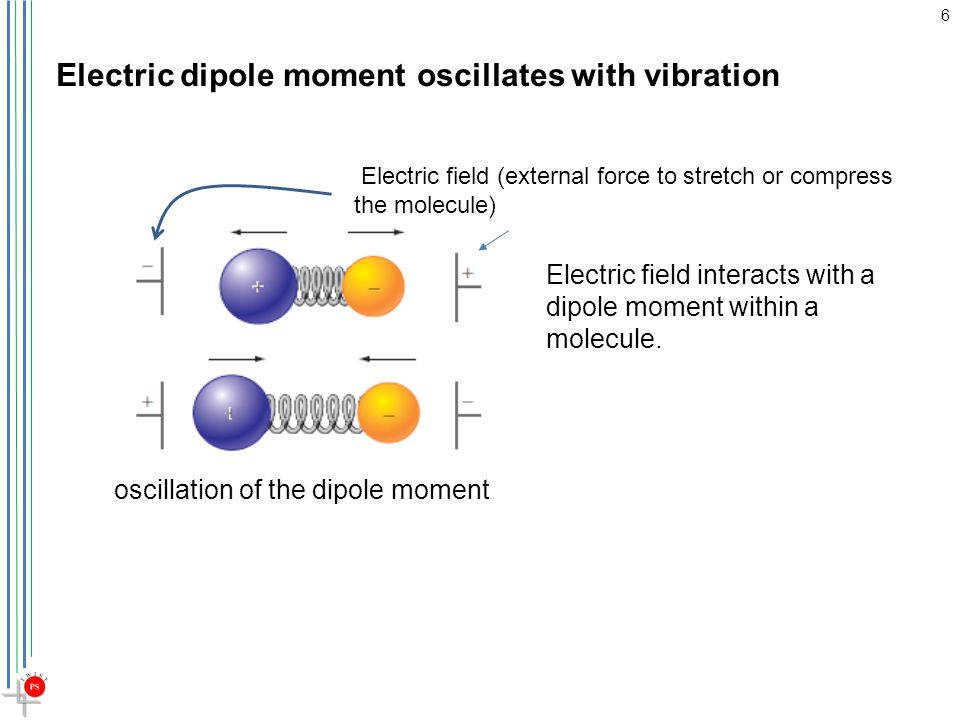
Thus, an external field can interact with the oscillating dipole.

If the external field has the same frequency as the oscillating dipole, there can be an energy exchange between the two systems.

Electromagnetic Waves

One component of an electromagnetic wave is an oscillating electric field.

Infrared absorption

If the frequency of the oscillating electric field equals the vibrational frequency of the bond, absorption of energy occurs.

The amplitude of the molecular vibration increases and the molecule is at a higher vibrational energy level.

The vibrational frequency of most bonds is roughly in the range of #10^13 color(white)(l)"Hz"# to #10^14 color(white)(l)"Hz"#. This is the infrared region of the electromagnetic region.

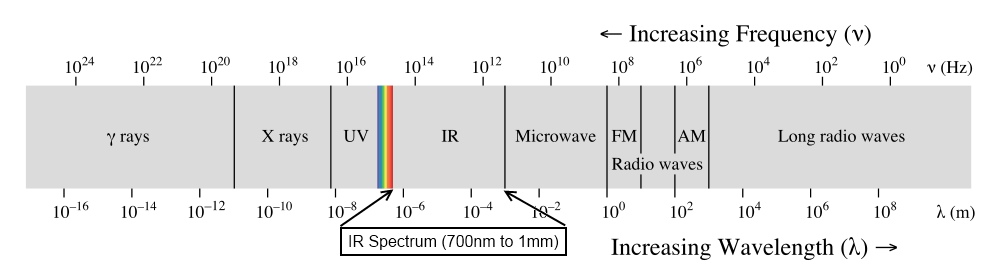
Thus, the study of molecular vibrations depends on the interaction infrared radiation with oscillating dipoles.

There's really not a nice and easy reason why.

In order for an infrared peak to be visible DUE TO infrared absorption, the dipole moment must change, because the normal modes of vibration, which belong to certain symmetries, are mutually orthogonal.

This can be seen if we take any two rows on a character table of different symmetries and take their dot product. Consider water for an example:

That is, if we took #Gamma(A_1) cdot Gamma(B_2)#:

#Gamma(A_1)cdotGamma(B_2) = Gamma(nu_2) cdot Gamma(nu_3)#

#= (1 cdot 1) + (1 cdot -1) + (1 cdot -1) + (1 cdot 1) = 0#

and that by definition makes them mutually orthogonal (their dot product is zero).

Seeing that, we consider that the transition moment probability is:

#M(nu -> nu') = int_(-oo)^(oo) psi^"*"(nu')hatmupsi(nu)dx ne 0#

UNLESS the dipole moment operator #hatmu# is a constant.

If #(dmu)/(dx) ne 0# (i.e. the dipole moment changes), then #hatmu# is an operator that is NOT a constant, which returns a nonzero probability for the infrared transition to occur.

This means that if the dipole moment doesn't change, #hatmu# is a constant, and

#muint_(-oo)^(oo) psi^"*"(nu')psi(nu)dx = 0#,

so that no infrared peak is seen.