What is the probability that an electron energy state in #"Ge"# will be occupied at temperature #"Τ = 300 Κ"# if the energy state is greater than the Fermi energy by #"2 eV"#?

The probability of electronic states occupied above the Fermi level is given by (derived below):

#f(epsilon_i) = 1/(1 + e^((epsilon_i - epsilon_F)//k_BT)#

I got #f(epsilon_F + "2 eV") = 2.54 xx 10^(-34)#.

If I plot the fraction of occupied states #f(epsilon_i)# vs. the energy relative to the Fermi energy #epsilon_i - epsilon_F# in #"eV"#, I get:

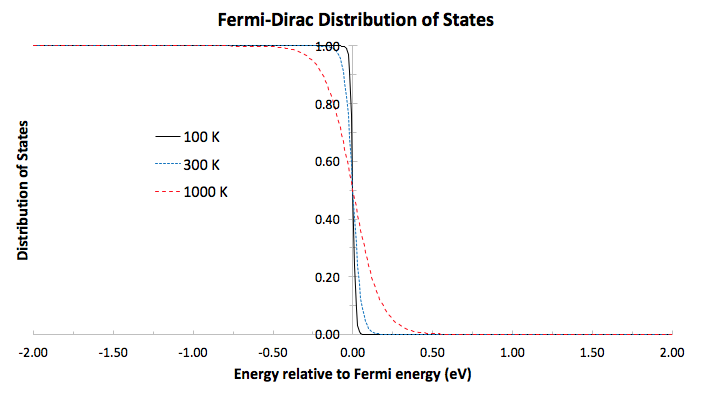
Here the graph shows #"100 K"#, #"300 K"#, and #"1000 K"#.

We should notice that at higher temperatures, a wider spread of energy levels around the Fermi level are occupied, consistent with an increase in system entropy with increasing temperature.

DISCLAIMER: LONG DERIVATION AHEAD!

We begin from the general case, where particles follow a distribution given either by Fermi-Dirac, Bose-Einstein, or corrected-Boltzon statistics.

This distribution is given by (Norman Davidson, Statistical Mechanics, pg. 78):

#lnt = sum_i (pm g_i ln((g_i pm N_i)/g_i) + N_i ln((g_i pm N_i)/N_i))#

where #N_i# is the number of particles in state #i# with energy #epsilon_i# of degeneracy #g_i#.

(For Fermi-Dirac particles, we take the lower sign. For Bose-Einstein particles, we take the upper sign.)

Suppose these particles are within a conservative system under the constraints of constant mass and energy:

#sum_i N_i = N#, the total number of particles

#sum_i N_iepsilon_i = E#, the total energy of these particles

Then, when the system is in equilibrium, all the particles are in the most probable distribution, and the Lagrangian can be written using the above constraints:

#ℒ = lnt + alphasum_i N_i - betasum_i N_iepsilon_i#

where #alpha# is an unknown constant for now, and #beta = 1//k_BT# is the reciprocal Boltzmann factor (a constant).

Maximizing the Lagrangian with respect to the number of particles in the most probable state #N_i^"*"#, we take the derivative w.r.t. #N_i#, defined at #N_i = N_i^"*"#, leaving #N_(j ne i)# constant, and set it equal to zero:

#(del ℒ)/(delN_i) = (del lnt)/(delN_i) + alpha (del)/(delN_i)[sum_i N_i] - beta (del)/(del N_i)[sum_i N_iepsilon_i] = 0#

Insert #lnt# to get (noting that terms in the sum associated with #N_(j ne i)# vanish):

#[cancel(-g_i cdot g_i/(g_i - N_i) cdot -1/(g_i)) + cancel(ln((g_i - N_i)/g_i)cdot0)^(0) + cancel(N_i cdot N_i/(g_i - N_i) cdot -g_i/N_i^2) + ln((g_i - N_i)/g_i)] + alpha - betaepsilon_i = 0#

#=> ln((g_i - N_i)/N_i) = ln(g_i/N_i - 1) = -alpha + betaepsilon_i#

The number of particles in the most probable state #i# is then given by:

#N_i^"*" = g_i/(1 + e^(-alpha)e^(betaepsilon_i))#

As it turns out, the constant we didn't know was #alpha = mu/(k_BT)# (we will not derive that here. See pp. 92 - 93 of this book), where #mu# is the chemical potential.

Now consider the Fermi function #f(epsilon_i)#, which describes the probability of finding Fermi-Dirac particles (e.g. electrons, which are fermions) at a certain energy level relative to #mu#.

It is given by the fundamental distribution law, #N_i/g_i#, where #N_i# is as was given for Fermi-Dirac particles:

#color(green)(f(epsilon_i)) = N_i/(g_i)#

#= 1/(1 + e^(-alpha)e^(betaepsilon_i)) = 1/(1 + e^(-mu//k_BT)e^(epsilon_i//k_BT))#

#= color(green)barul(|stackrel(" ")(" "1/(1 + e^((epsilon_i - mu)//k_BT))" ")|)#

At #T = "0 K"#, #mu = epsilon_F#, the Fermi energy, while #epsilon_i# is some energy level relative to the Fermi level. The energies below the Fermi energy ought to be #100%# occupied at #"0 K"#.

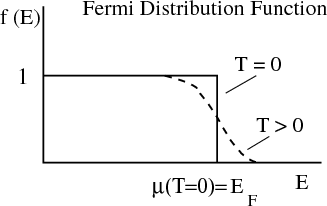
To find the probability of occupying an energy level #epsilon_i = epsilon_F + "2 eV"#, i.e. ABOVE the Fermi energy, we just insert #epsilon_i# as follows:

#f(epsilon_F + "2 eV") = 1/(1 + e^(("2 eV")//k_BT))#

In #"eV"#, the value of the Boltzmann factor at #"300 K"# is:

#k_BT = 1.38065 xx 10^(-23) cancel"J""/"cancel"K" xx 300 cancel"K" xx ("1 eV")/(1.602 xx 10^(-19) cancel"J")#

#=# #"0.02585 eV"#

Therefore:

#color(blue)(f(epsilon_F + "2 eV")) = 1/(1 + e^(2//0.02585))#

#=# #color(blue)(2.54 xx 10^(-34))#

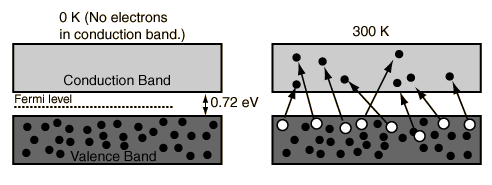
Since germanium has an actual band gap around #"0.72 eV"# at #"300 K"#, we were apparently looking for states above the conduction band by #2 - 0.72/2 = "1.64 eV"#.

At room temperature, that isn't likely to be well-populated by default.