When 0.602 g of biphenyl (C12H10) undergoes combustion in a bomb calorimeter, the temperature rises from 26.5 ∘C to 30.4 ∘C. What is the ΔErxn for the combustion of biphenyl? The heat capacity of the bomb calorimeter is 5.86 kJ/∘C.

#DeltaE_"rxn" = -5.85 xx 10^3 "kJ/mol"#

What is this value in #"kJ/g"#?

A bomb calorimeter operates at constant volume, i.e. it is rigid.

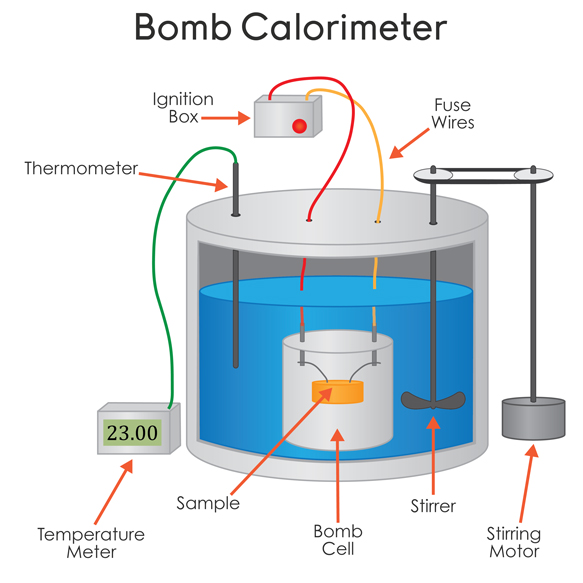
The biphenyl is placed into the sample holder and ignited from the outside. The temperature of the water inside (typically approx. #"2 L"#) will rise, as the reaction releases heat, and the cited heat capacity accounts for both the dry device and the water .

At constant volume, we obtain from the first law of thermodynamics:

#DeltaE = q + w#

#~~ q - cancel(PDeltaV)^(0)#

#-= q_V#

where #q_V# is the heat flow out from the reaction towards the surrounding water at constant volume.

By unit conversion (no equation required),

#q_V = "5.86 kJ"/cancel(""^@ "C") xx (30.4cancel(""^@ "C") - 26.5cancel(""^@ "C"))#

#=# #"22.9 kJ" = DeltaE_"soln"#

due to combusting #"0.602 g biphenyl"#. By conservation of energy,

#q_V + q_"rxn" = 0#

Therefore,

#q_V -= DeltaE_"soln" = -q_"rxn" -= -DeltaE_"rxn"#

and from this,

#color(blue)(DeltaE_"rxn") = -q_V/(n_"reactant")#

#= -("22.9 kJ")/(0.602 cancel"g biphenyl") xx (154.21 cancel("g C"_12"H"_10))/"1 mol"#

#= color(blue)(-5.85 xx 10^3 "kJ/mol")#