What is the electron count for these complexes??

Starred are the central atoms.

#"Cp"_2stackrel("*")"Ta"("CH"_2)_2stackrel("*")"Ir"("CO")("PPh"_3)#:

#14e^(-) + 16e^(-)# (respectively for each metal center)

#"Ph"_2stackrel("*")"P"("CH"_2)_2stackrel("*")"Ir"("CO")("PPh"_3)#:

#8e^(-) + 16e^(-)# (respectively for each central atom)

Drawing out the first molecule, I get:

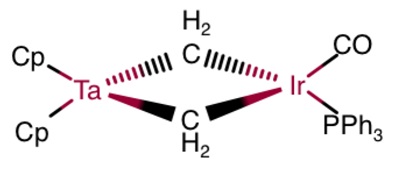
The second molecule is isostructural with the first.

DONOR-PAIR METHOD

• Using the Donor-Pair method, I would assign two electrons per #"CH"_2# bond, treating the #"CH"_2# carbenes as #-2# ligands that donate a total of #4# valence electrons, i.e. #""^((-2)):ddot"C""H"_2#. A #-1# charge is then given to each half of the complex per #"CH"_2#.

• Tantalum often forms the #+5# oxidation state, and iridium is fine with a #+1# oxidation state.

• #"Cp"# is #"C"_5"H"_5#, which as a 5-electron donor is #"C"_5"H"_5^(-)#, cyclopentadienyl anion.
• #"CO"# and #"PPh"_3# are both 2-electron #sigma# donors and #pi# acceptors.

From this, around the tantalum center we have:

#"Ta"^(+5):# #0e^(-)# (noble gas configuration)
#2 xx "Cp":# #2xx5e^(-)#
#ul(2 xx "CH"_2: 2xx2e^(-))# (2 per bond)
#"Total" = 14e^(-)#

The total charge adds up around the tantalum center as #5-1-1-1-1 = +1#.

From this, around the iridium center we have:

#"Ir"^(+1):# #8e^(-)# (one #6s# and seven #5d# electrons)
#"CO":# #2e^(-)#
#"PPh"_3: 2e^(-)#
#ul(2 xx "CH"_2: 2xx2e^(-))# (2 per bond)
#"Total" = 16e^(-)#

The total charge adds up around the iridium center as #1 + 0 + 0 - 1 - 1 = -1#. This combines with the tantalum center to give a neutral complex overall.

NEUTRAL LIGAND METHOD

If you want to do a different electron-counting method (the Neutral Ligand Method)...

If #"Ir"# is given the oxidation state of #-1# based on the charge of the complex (would we know this ahead of time? Perhaps), and the ligands are neutral, then what changes is that the carbenes are singlet carbenes, #:"CH"_2#, that donate one electron per bond.

Around #"Ta"# we would assign a #+1# oxidation state if we already know that the charge of that half is #+1#, and then the ligands are presumed neutral. As a result, #"Cp"# becomes a #4e^(-)# donor.

The result is then:

#"Ta"^(+1):# #4e^(-)# (noble gas configuration)
#2 xx "Cp":# #2xx4e^(-)#
#ul(2 xx "CH"_2: 2xx1e^(-))# (1 per bond)
#"Total" = 14e^(-)#

#"Ir"^(-1):# #10e^(-)# (one #6s# and seven #5d# electrons)
#"CO":# #2e^(-)#
#"PPh"_3: 2e^(-)#
#ul(2 xx "CH"_2: 2xx1e^(-))# (2 per bond)
#"Total" = 16e^(-)#

And that's good, we got the same result in the end. It should not matter either way.

I'll leave it to you to do #"Ph"_2"P"("CH"_2)_2"Ir"("CO")("PPh"_3)#. Assume phosphorus is the #+5# oxidation state and iridium is the #+1# oxidation state. That will again give a #+1# charge to the left half and a #-1# charge to the right half.

You should get #8# electrons around phosphorus and #16# electrons around iridium again.