It's associated with its magnetic quantum number, #m_l#.
A given set of atomic orbitals specified by the angular momentum quantum number #l# has #2l + 1# degenerate orbitals (of equal energy), each of which corresponds to a unique #m_l# in the set #{-l, -l+1, . . . , 0, . . . , l-1, l}#.
For example, given the so-called #2p# subshell, we have that #l = 1# for all #2l+1 = "three"# #2p# atomic orbitals of principal quantum number #n#.
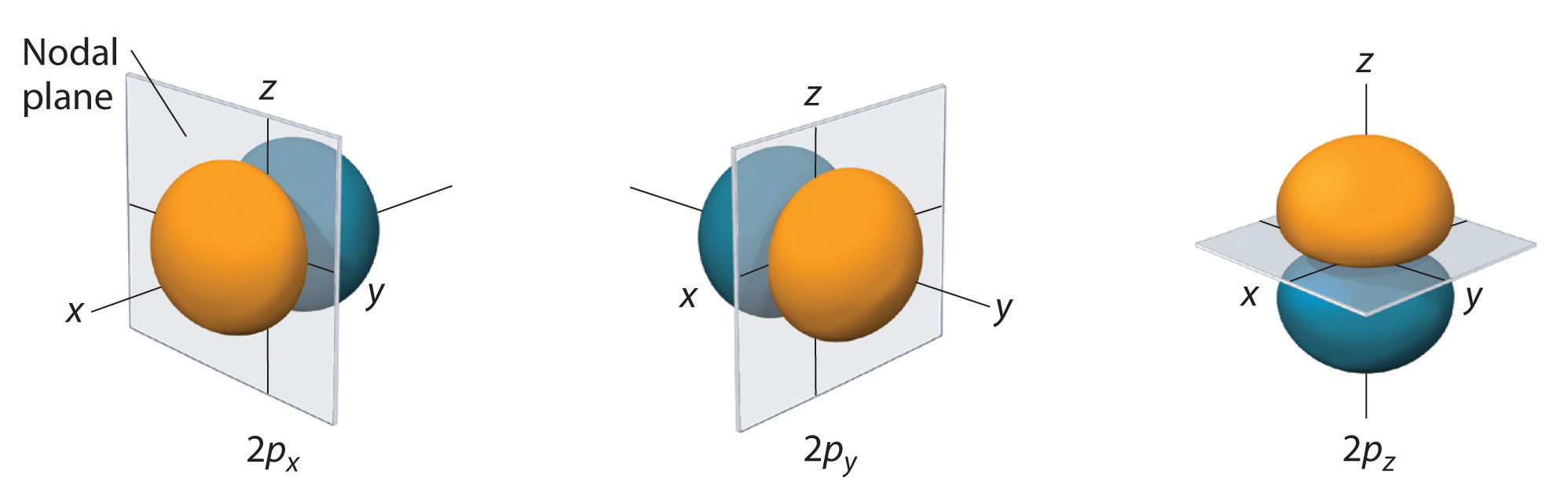
These #2p# atomic orbitals correspond to the magnetic quantum numbers #m_l = {-1,0,+1}#, correlating with having #"three"# #2p# orbitals. We arbitrarily assign #m_l = 0# to the #2p_z#, and thus either the #2p_x# or #2p_y# can have #m_l = +1# while the remaining one gets #m_l = -1#.


