PLEASE Help! with Reactants decreasing in Molarity?

Question

Rate constant = 0.80 M^-1 s^-1 at 300℃
2nd order Reaction

Calculate the time it takes for the Initial reactant concentration to decrease from 0.072M to 0.054M

Please Help by showing my how to tackle this equation in steps! Thank you!
Always,
Ozzy

288 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-17T03:46:05

I got about #"4.34 s"#.

Set up the rate law.

#r(t) = k[A]^2#

as it would be for a second order reaction with one reactant. I assume you mean

#A -> B#

To solve this, you only have the rate constant #k# and two concentrations, so you need the initial rate.

The initial rate of reaction ought to be near the start of the reaction, and you were given

#Delta[A] = "0.072 M" - "0.054 M"#

The tangent line that touches the start of reaction has to touch #[A] = "0.072 M"# at #t = "0 s"#.

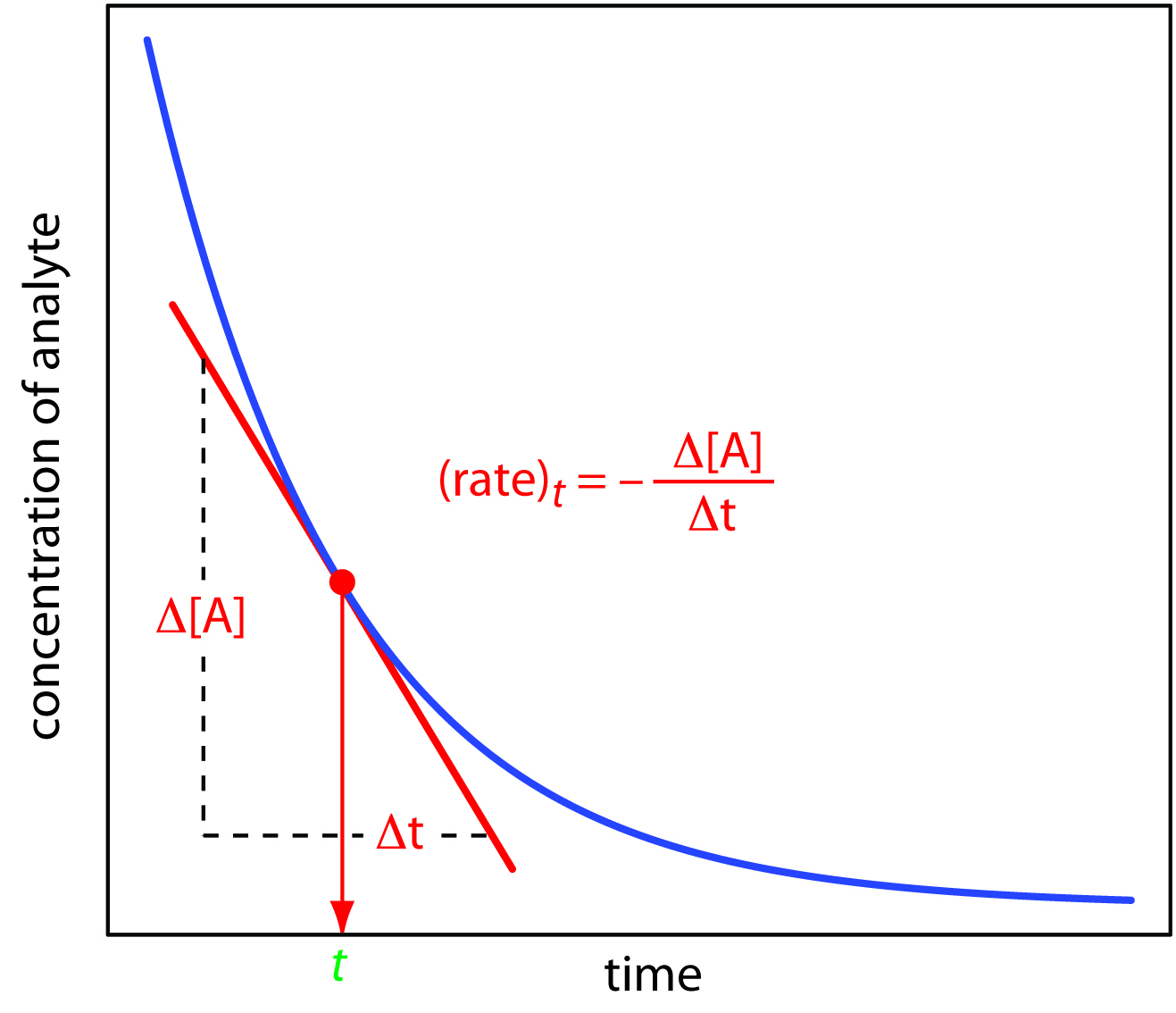
Assuming #Delta[A]# is small, that part of the curve is straight, i.e.

#-(Delta[A])/(Deltat) ~~ r(t)#

We assume that the coefficient of #A# is #1#... The starting concentration is #"0.072 M"#, so we pick that to calculate the initial rate:

#r(t) ~~ "0.80 M"^(-1)cdot"s"^(-1)("0.072 M")^2#

#= 4.15 xx 10^(-3) "M/s"#

Now we can equate that to the change in concentration over time in this presumably short time interval.

#-(Delta[A])/(Deltat) ~~ 4.15 xx 10^(-3) "M/s" ~~ -("0.054 M" - "0.072 M")/(Deltat)#

Therefore:

#color(blue)(Deltat) ~~ -("0.054 M" - "0.072 M")/(4.15 xx 10^(-3) "M/s")#

#=# #color(blue)("4.34 s")#