Is this right? Lim using derivative?
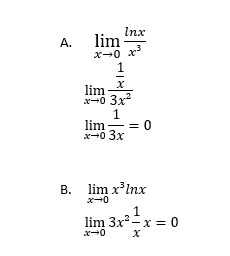
1 Answer
Well, no.
L'Hopital's rule on
#A# , since it is of the form#-oo/0# , would not apply. It only applies with#oo/oo# or#0/0# .Try applying the limit product rule:
#= lim_(x->0) lnx lim_(x->0) 1/x^3# The second limit has two options.
- From the left,
#lim_(x->0^(-)) 1/x^3# approaches#-oo# .- From the right,
#lim_(x->0^(+)) 1/x^3# approaches#oo# .So, noting that
#x# can only approach#0# from the right in#lnx# :
#L = lim_(x->0^(pm)) lnx cdot lim_(x->0^(pm)) 1/x^3#
#(1) = # #color(red)("DNE")# if approaching both limits from the left
#(2) = # #color(red)(oo)# if approaching the first limit from the right and the second limit from the left
#(3) = color(red)(-oo)# if approaching both limits from the rightHere we assume that the limit product rule requires both limits to be approached from the same direction.
So then, whether we accept the combination of options
#(1)# and#(3)# , or#(2)# and#(3)# , we still get two different results from both directions, and the overall limit does not exist.
Here you can rewrite this as:
#lim_(x->0) x^3lnx#
#= lim_(x->0) x^3 cdot lim_(x->0) lnx# where we have the form
#0 cdot -oo# .We cannot apply L'Hopital's rule yet (if at all!). Instead, try dividing by
#1/x^3# to get:
#L = lim_(x->0) (lnx)/(1//x^3)# Now we have the form
#-oo/(pmoo)# , so you have two options for the limit...
#lim_(x->0^(-)) (lnx)/(1//x^3) = "DNE"# , because you can't approach#lnx# from the left of#0# (the domain is#(0,oo)# ).On the other hand...
#color(blue)(lim_(x->0^(+)) (lnx)/(1//x^3))# can be done using L'Hopital's rule, since the negative of the limit is of the form#oo/oo# .
#= lim_(x->0^(+)) (1//x)/(-3//x^4)#
#= lim_(x->0^(+)) -x^3/3#
#= color(blue)(0)# Again, note that this limit only exists due to approaching from the right, not the left.

