How are torque and force similar? How are they different?

Force is in general translational (along a straight line; vectorial), while torque is angular, or rotational (the only effective component is the one perpendicular to a lever arm).

Force in the general sense is a vector influence that accelerates or decelerates a mass, and is given in #"N"#, or #"kg"cdot"m/s"^2#. The force can be seen in Newton's second law:

#vecF = mveca = mddotq#,

where #q# is the general position coordinate, #ddotq = (del^2q)/(delt^2)#, and #veca# is acceleration in #"m/s"^2#. #m# is mass in #"kg"#.

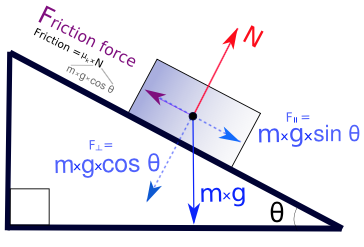
When one takes the cross product with the distance #vecr# away from a central object, we get the torque, the vector influence that rotates an object about a center by rotating its lever arm:

#vectau = vecr xx vecF#

#= |r| cdot |F| cdot sintheta = |r| cdot F_(_|_)#,

where #theta# is the angle between #vecF# and the lever arm. You can see only the perpendicular component of #vecF# imparts torque.

Torque is also a vector, since it is due to a cross product of two vectors, but is angular in character. We also see torque written as:

#vectau = I vecalpha#,

where #vecalpha# is the angular acceleration in #"rad/s"^2# and #I# is the moment of inertia in #"kg"cdot"m"^2#. This can be seen as the rotational analogue of Newton's second law.