A 1956 dime is made of a silver-copper alloy and has a mass of 2.490. The dime was dissolved in nitric acid and a blue solution remained. The solution quantitatively transferred to a 100mL volumetric flask and brought to volume with water...?

Method #b# is more accurate if the actual percent by mass is #"90 % w/w Ag"#, but is more prone to experimenter error than experimental/random error.

The blue solution that forms due to dissolving the dime in #"HNO"_3# follows the nitric acid reduction and copper oxidation given here:

#2("NO"_3^(-)(aq) + 4"H"^(+)(aq) + cancel(3e^(-)) -> "NO"(g) + 2"H"_2"O"(l))#
#3ul(("Cu"(s) -> "Cu"^(2+)(aq) + cancel(2e^(-)))" "" "" "" "" "" "" "" ")#
#2"NO"_3^(-)(aq) + 3"Cu"(s) + 8"H"^(+)(aq) -> 3"Cu"^(2+)(aq) + 2"NO"(g) + 4"H"_2"O"(l)#

A #color(blue)("blue")# copper solution is due to #"Cu"^(2+)# (a red solution would be due to #"Cu"^(+)#). #"Ag"(s)# also gets dissolved in this way. I'll leave it to you to write the reaction this time.

These both occur because nitrate reduction is more favorable than silver and copper reduction (its #E_(red)^@# is more positive).

#a)#

If #"50.00 mL"# of the original #"100.00 mL"# in the volumetric flask (which was made to contain #"100.00 mL"#!) was titrated with excess #"NaCl"#, then all of the #"Ag"^(+)# will precipitate with the #"Cl"^(-)# in the form of #"AgCl"(s)#.

Upon washing, filtering, drying, weighing, drying, weighing, drying, etc... a mass of #"1.375 g"# recovered of #"AgCl"# would suggest that:

#1.375 cancel"g AgCl" xx "107.8682 g Ag"/(143.32 cancel"g AgCl") = "1.035 g Ag"^+#

And this mass of silver cation was what reacted with the #"NaCl"# from within the #"50.00 mL"# aliquot.

Therefore, since volume and mass are extensive, we really have #ul("2.070 g Ag"^(+))# dissolved in the original flask volume, and as a result, the percent by mass of #"Ag"# metal in the alloy is:

#"2.070 g Ag"/"2.490 g alloy" = color(blue)(83.12% "w/w Ag")#

Errors in this method include:

• loss of solid in filtration into the Erlenmeyer flask
• loss of solid due to not washing all of it into the filter paper
• dropping solid flakes of #"AgCl"# on the ground

All of these lead to a less than #100%# mass yield.

#b)#

Using the given standard curve from the data previously collected:

#ul("Conc. (mg/mL)"" ""A""bsorbance")#
#5.00" "" "" "" "" "" "0.843#
#4.00" "" "" "" "" "" "0.672#
#3.00" "" "" "" "" "" "0.507#
#2.00" "" "" "" "" "" "0.336#
#1.00" "" "" "" "" "" "0.161#

we would construct an Excel graph to obtain #y = 0.1700x - 0.0062# for the Beer's law fit line equation:

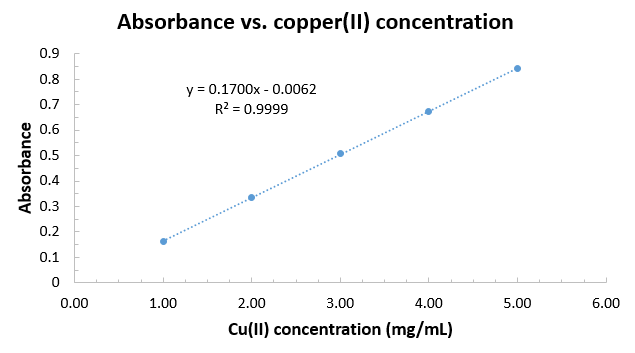
And hence, with the absorbance of #"Cu"^(2+)# being #0.420# for #lambda_(max) = "740 nm"# (absorbing red light, reflecting blue), we use Beer's Law to get:

#A = epsilonbc + y"-int"#

#=> color(blue)(c) = (A - y"-int")/(epsilonb)#

#= (0.420 -(- 0.0062))/(0.1700) "mg"/"mL"#

#=# #"2.507 mg Cu"^(2+)"/mL"#

#=# #"250.7 mg Cu"^(2+)"/100 mL"#

#=# #color(blue)("0.2507 g Cu"^(2+)"/100 mL")#

By subtraction,

#"2.490 g" - "0.2507 g Cu" = "2.239 g Ag"#

Thus,

#"2.239 g Ag"/"2.490 g alloy" = color(blue)(89.93% "w/w Ag")#

This method is not void of errors. They include:

• Wrong choice of wavelength (it is a reasonable wavelength)
• Calibrating with the measured sample each time, making all the absorbance values too low (yes, students do this)
• Spilling sample into the spectrophotometer, saturating the absorbance readings (quite possible)

Of course, if all of these are done right, then this is quite accurate.