It depends on the pKa difference between the Lewis acid (such as ethanamine/ethylamine) and the conjugate acid of the Lewis base (such as #H_2O# relative to #OH^(-)#).
Neutral ethylamine has a #"pKa"# of almost #40# in water (recall the #"pKa"# of ammonia is #36#), and water has a #"pKa"# of #15.7#.
A lower #"pKa"# indicates a stronger acid (i.e. a weaker bond) or a weaker base.
If ethylamine and #"OH"^(-)# were to react substantially, then the conjugate acid of #"OH"^(-)#---which is water---would have to have a substantially higher pKa than #40# because the equilibrium lies on the side of the weaker acid.
Water would have to be a weaker acid than ethylamine for a large percent of it to be protonated, but it's not. Its #"pKa"# is much lower than #40#, so it's a stronger acid, and a large percent of the water is not in the #"H"_2"O"# form, but #"OH"^(-)#.
Their reaction would look like this:
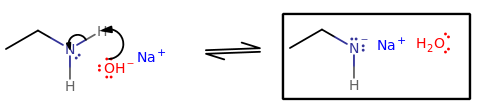
But just how substantial is it? Consider the equilibrium here where ethylamine acts as an acid:
#"K"_a = (["CH"_3"CH"_2"NH"^(-)])/(["CH"_3"CH"_2"NH"_2]["OH"^(-)])#
Let's assume the #"pKa"# is #40#. Then #10^(-40) = "K"_a#. We know that's very small, so for practical intents and purposes, we can say that ethylamine does not react with #"NaOH"#.
On the other hand, if the other reactant were to be #"H"_3"O"^(+)#, then yeah, that would work. The #"pKa"# of #"H"_3"O"^(+)# is about #-1.7#, which means it is a stronger acid than #"CH"_3"CH"_2"NH"_3^(+)#, whose #"pKa"# is about #10.7#. Therefore, ethylamine can steal a proton and a substantial percent of protonated ethylamine exists.


