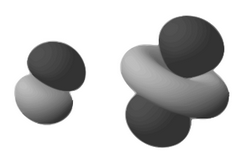
d_z2 orbital participate in sp^3d hybridization and not any other d-orbital.why?

Because the resultant trigonal bipyramidal geometry of the hybrid orbitals requires both lobes to be the same phase on the #z# axis, and requires five total orbitals.

To form the trigonal bipyramidal electron geometry with five hybrid orbitals, we need to put in five orbitals:

#1 xx ns#

#+ 1 xx np_x#

#+ 1 xx np_y#

#+ 1 xx np_z#

#+ 1 xx (n-1)d_(z^2)#

#-> 5 xx sp^3d#

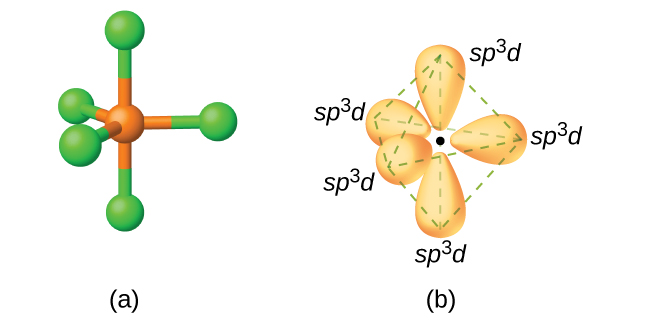
• Every hybrid orbital needs an #s# orbital contribution. It's always there for "completeness".
• #p_x# and #p_y# allow bonding on the #bb(xy)# plane, to give three identical directions when you include the #s# orbital.
• #p_z# allows bonding in a third dimension, but does not support identical bonds on both ends of the #z# axis (it has opposite phases on each lobe).
• The #d_(z^2)# provides the same orbital phase in both the #z# directions, which the #p_z# does not provide.

Had we chosen #d_(x^2-y^2)#, one of the bonds made would be unlike the others, and bonding in the #xy# plane would be more stable than bonding along the #z# axis. [The #d_(xy)#, #d_(xz)#, and #d_(yz)# don't fit here, because they are meant for #pi# or #delta# bonding, not #sigma# bonding.]

It's kind of like #sp# hybridization in #"H"-"C"-="C"-"H"#. Each central carbon needs two #sp# hybrid orbitals, which consist of #s+p_z#, to bond identically in both directions. They can't simply use pure #p_z# orbitals, which have lobes of opposite phase.

Both lobes have to be the same phase to minimize creation of nodes, which would have made the structure higher in energy than it needed to be if they were there.