Derive the charge to mass ratio (#e//m#) for an electron?

For an electron, the mass to charge ratio is:

#= (-|e|)/m = -(E)/(B^2r)#

with #e = 1.602 xx 10^(-19) "C"# being the elementary charge. #r# is the radius of helical motion; #E# and #B# are the electric and magnetic field strengths, respectively.

DISCLAIMER: LONG ANSWER!

WHY AN ELECTRON INTERACTS WITH A MAGNETIC FIELD

If you recall from chemistry, every electron has an intrinsic magnetic moment---that's what gives it its "spin-up" (#m_s = +1/2#) or "spin-down" (#m_s = -1/2#) orientation.

It's why we represent them as #uarr# or #darr# in orbitals.

When you send an electron shooting into a magnetic field, its intrinsic magnetic moment interacts with the magnetic force imparted by the field, and the electron begins to move in a circular path.

The magnetic force makes the particle move in a circular path, and the forward momentum of the particle is what projects the circular path into helical motion.

LORENTZ FORCE & MAGNETIC FIELD

This kind of motion is described by:

#\mathbf(vecF_B = qvecvxxvecB#

where:

• #q# is the charge of the moving particle.
• #vecv# is the velocity of the particle, tangent to the circular path.
• #vecF_B# is the magnetic force imparted by the magnetic field, perpendicular to the velocity of the particle. Its direction depends on the charge of the particle as well as the direction of #vecB#.
• #vecB# is the magnetic field itself, which is perpendicular to #vecv# and #vecF_B#.

When we evaluate the cross product, note the definition of the cross product:

#veca xx vecb = ||veca||*||vecb|| sintheta*vecu#

where #vecu# is the unit vector that accounts for which direction #vecB# goes, based on the right hand rule.

Applying this definition, we get (for #qvecv = veca# and #vecB = vecb#):

#=> \mathbf(vecF_B = qvecv Bsintheta)#

#theta = 90^@ => sintheta = 1#.

LORENTZ FORCE WITH POSITIVELY-CHARGED PARTICLES

Let's apply this for when #vecB# is going away from us, and then when #vecB# is going towards us, for a positively-charged particle.

For a negatively-charged particle, the direction of motion (CW/CCW) is opposite.

Since for a positively-charged particle, the helix is CCW, the electron would move in a CW helix if the magnetic field is moving away from us.

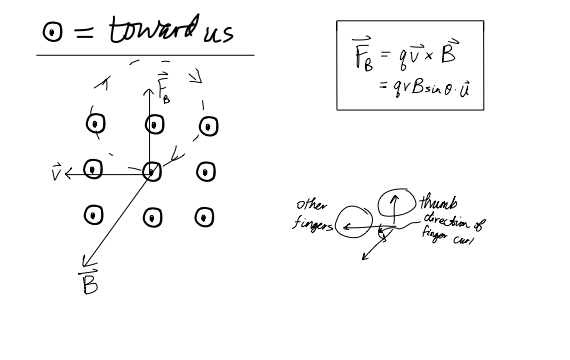
Since for a positively-charged particle, the helix is CW, the electron would move in a CCW helix if the magnetic field is moving towards us.

RELATING LORENTZ FORCE BACK TO UNIFORM CIRCULAR MOTION

In a uniform magnetic field, this is uniform circular motion, which means that for the electron (or any charged particle), we can equate this behavior back to the sum of the centripetal forces:

#sum vecF_c = vecF_B = (-q)vecvB = (mv^2)/vecr#

#=> color(blue)(vecr = -(mvecv)/(qB))#

From this we can say:

• For a larger particle, the radius of deflection from the path of the magnetic field is larger.
• For a smaller particle, the radius of deflection from the path of the magnetic field is smaller.
• For a positively-charged particle, the path of helical motion is CCW for a magnetic field moving away from us.
• For a negatively-charged particle, the path of helical motion is CW for a magnetic field moving away from us.
• The sign of #vecr# tells us whether the motion is CW/CCW, or the opposite (CCW/CW), but #vecr# always points inwards.

CHARGE-TO-MASS RATIO

The charge-to-mass ratio #e/m# is derived as follows. In a magnetic and electric field, we start from what we had before:

#qvecvxxvecB = (mv^2)/vecr#

Recall that the electric force is #vecF_E = qvecE#.

For a positively-charged particle:

#vecF_E = qE = vecF_B = qvB#

#=># #v = E/B#

where we have focused the electric and magnetic field directions and used their magnitudes.

Plugging this back into the circular motion equation:

#qE = (mE^2)/(rB^2)#

#q/m = (E)/(B^2r)#

#=> color(blue)(e/m = -(E)/(B^2r))#

From this equation, we find that the more massive the particle, the larger the radius of deflection must be.

This is actually what we determined earlier, though, so it makes sense that we concluded the same thing again.