Write out the symmetry elements and operators for cyclopentane, and determine its point group?

I assume you mean a pentagon... if not, ask for the conformations...

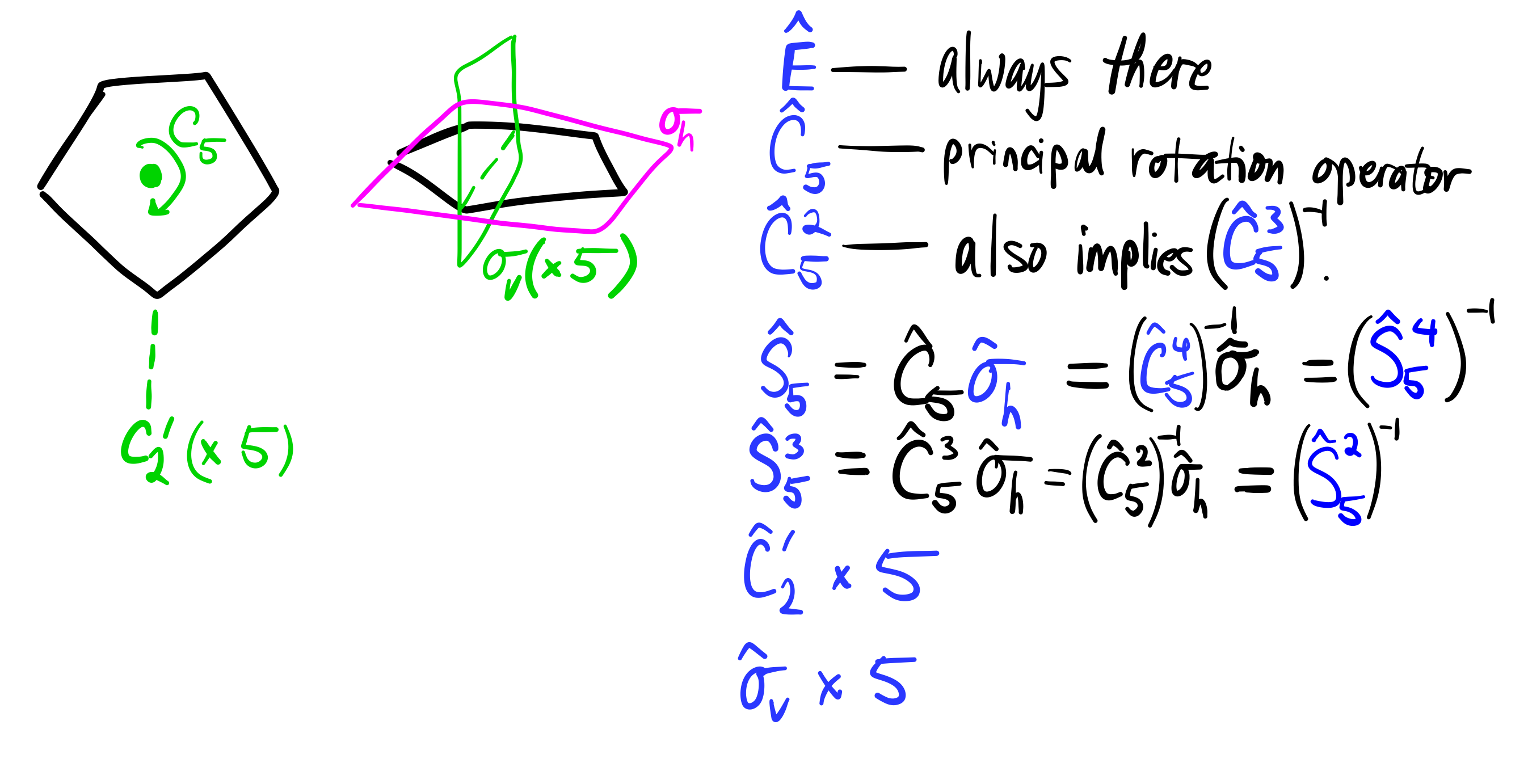
• Every molecule has an identity element #E#, with corresponding operator #color(blue)(hatE)#.
• This pentagon has a five-fold rotational axis element, i.e. #C_5# axis on the #z# axis, and the corresponding #color(blue)(hatC_5)# operator .

If there's a #hatC_5#, there's a #color(blue)(hatC_5^2)# (as you can do the same thing twice). Also, #color(blue)(hatC_5^3) = (hatC_5^2)^(-1)# is also included, and #color(blue)(hatC_5^4) = hatC_5^(-1)# is included. Why are they inverses?

• There is a horizontal mirror plane element #sigma_h# with corresponding operator #color(blue)(hatsigma_h)#.

If there is both #hatC_n# and #hatsigma_h#, then there also exists #hatS_n#, the improper rotation operator. Its corresponding individual elements have already been mentioned... and the operator is then #color(blue)(hatS_5)#.

If there is #hatS_5#, then there is #color(blue)(hatS_5^3)#. That means we also include #color(blue)(hatS_5^2)# as the inverse of #hatS_5^3#, and #color(blue)(hatS_5^4)# as the inverse of #hatS_5#.

• There are also FIVE #C_2'# rotation axis elements coplanar with the plane of the molecule, one of which is along the #x# axis. It corresponds to the #color(blue)(hatC_2')# operator, one for each element.

• There are lastly FIVE #color(blue)(sigma_v)# vertical mirror plane elements perpendicular to the plane of the molecule (corresponding to the #hatsigma_v# operator), one of which is on the #xz# plane.

That gives #bb20# total symmetry elements, and #bb12# total symmetry operators. Eight of these are duplicate operators #hatC_2'# and #hatsigma_v# that correspond to applying #hatC_5# on each of them #1-3# times.

Upon knowing that there exist #hatC_5#, #sigma_h#, and #hatC_2'# operators that leave the molecule invariant, it follows that the point group is #bb(D_(5h))#. That is, #hatC_5 + hatsigma_h -> C_(5h)#, and #C_(5h) + hatC_2' -> D_(5h)#.

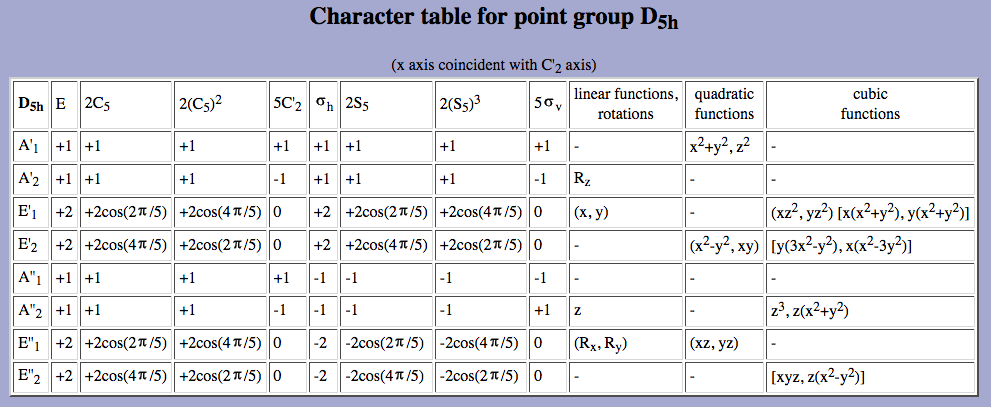
This is summarized in the character table: