Answer these questions about glycine?

#a)#

Glycine is the simplest amino acid, containing two #"H"# atoms on its #alpha# carbon:

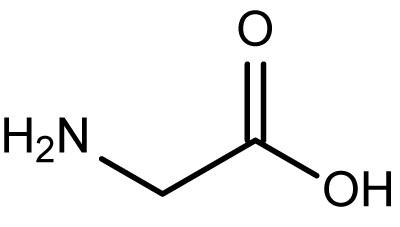
The carboxyl proton #"pKa"# is near #2.2#, and the amine proton #"pKa"# is around #9.8#. Thus,

• Below #"pH" ~~ 2.2#, the amine proton is ON, and the carboxyl proton is ON. This is the #"AA"^+# form.
• At #"pH" = 7.4# (body #"pH"#), the amine proton is ON, and the carboxyl proton is OFF. This is the #"AA"^0# form.
• Above #"pH" ~~ 9.8#, the amine proton is OFF, and the carboxyl proton is OFF. This is the #"AA"^-# form.

You can draw those by interpreting the notes above.

#b)#

The #"pH"# of #"0.1 M"# solutions of each of these forms is based on the #K_a# values. The most acidic form is #"AA"^+# and the most basic form is #"AA"^-#.

With #K_(a1) = 4.57 xx 10^(-3)# and #K_(a2) = 2.51 xx 10^(-10)#, the first one can be seen to belong to the carboxyl proton (why? It's higher, so it is ascribed to the more acidic proton). Treating glycine as a diprotic acid,

#"H"_2"Gly"^(+)(aq) rightleftharpoons "HGly"(aq) + "H"^(+)(aq)#

#"I"" "" ""0.1 M"" "" "" "" ""0 M"" "" "" "" ""0 M"#
#"C"" "" "-x" "" "" "" "+x" "" "" "" "+x#
#"E"" "(0.1-x)"M"" "" "" "x" M"" "" "" "x" M"#

And so, write the mass action expression:

#K_(a1) = 4.57 xx 10^(-3) = x^2/(0.1 - x)#

Naively using the small #x# approximation,

#4.57 xx 10^(-3) ~~ x^2/0.1#

#=> x_0 ~~ sqrt(4.57 xx 10^(-3) cdot 0.1) = "0.0214 M"#

That is not yet correct. We then generate our next guesses to converge onto the final #x#:

#=> x_1 ~~ sqrt(4.57 xx 10^(-3) cdot (0.1 - 0.0214)) = "0.0190 M"#
#=> x_2 ~~ sqrt(4.57 xx 10^(-3) cdot (0.1 - 0.0190)) = "0.0192 M"#
#=> x_3 ~~ sqrt(4.57 xx 10^(-3) cdot (0.1 - 0.0192)) = "0.0192 M"#

And so, #["H"^(+)] = "0.0192 M"#, giving

#color(blue)("pH") = -log(0.0192) = color(blue)(1.72)#.

The first conjugate base is a much weaker acid. Again, we treat this as in a separate solution:

#"HGly"(aq) rightleftharpoons "Gly"^(-)(aq) + "H"^(+)(aq)#

#"I"" "" ""0.1 M"" "" "" ""0 M"" "" "" ""0 M"#
#"C"" "" "-x" "" "" "+x" "" "" "+x#
#"E"" "(0.1-x)"M"" "" "x" M"" "" "x" M"#

And so, write the mass action expression:

#K_(a2) = 2.51 xx 10^(-10) = x^2/(0.1 - x) ~~ x^2/0.1#

Here, the small #x# approximation is justified; #K_(a2)# #"<<"# #10^(-5)#. Thus:

#x = ["H"^(+)] = sqrt(2.51 xx 10^(-10) cdot 0.1) = 5.01 xx 10^(-6) "M"#

And so,

#color(blue)("pH") = -log["H"^(+)] = -log(5.01 xx 10^(-6)) = color(blue)(5.30)#.

Its conjugate base is obviously a base, and so, treating this as in ANOTHER separate solution, we need the #K_b#.

At body temperature, #37^@ "C"#, #K_w = 2.42 xx 10^(-14)#, so:

#K_b = K_w/K_a = (2.42 xx 10^(-14))/(2.51 xx 10^(-10)) = 9.64 xx 10^(-5)#

This is still small enough for the small #x# approximation.

#"Gly"^(-)(aq) + "H"_2"O"(l) rightleftharpoons "HGly"(aq) + "OH"^(-)(aq)#

#"I"" "" ""0.1 M"" "" "" "-" "" "" ""0 M"" "" "" ""0 M"#
#"C"" "" "-x" "" "" "" "-" "" "+x" "" "" "+x#
#"E"" "(0.1-x)"M"" "" "-" "" "" "x" M"" "" "x" M"#

Just as before...

#K_b = 9.64 xx 10^(-5) = x^2/(0.1 - x) ~~ x^2/0.1#

Thus, since #["OH"^(-)] = sqrt(K_b["Gly"^(-)])#, the #["H"^(+)]# is:

#["H"^(+)] = K_w/(["OH"^(-)]) = (2.42 xx 10^(-14))/(sqrt(9.64 xx 10^(-5) cdot 0.1))#

#= 7.79 xx 10^(-12) "M"#

This gives a #"pH"# of

#color(blue)("pH") = -log(7.79 xx 10^(-12)) = color(blue)(11.1)#