Calculate the change in freezing point for ice if the pressure changes from #"1 atm"# to #"3 atm"#?
#DeltaH_"fus" = 796 cdot 4.186 cdot 10^7 "erg/g"#
Specific volume of ice = #"1.0001 cm"^3"/g"#
Specific volume of water = #"1.0908 cm"^3"/g"#
Specific volume of ice =
Specific volume of water =
1 Answer
#DeltaT_f ~~ -0.015^@ "C"#
This change was so small since the solid-liquid coexistence curve is often very steep. So the small pressure change typically doesn't alter the melting point that much.
A few things to keep in order:
- Seems like there's a typo. There are
#10^10 "ergs"# in#"1 kJ"# , so you should have had#DeltaH_"fus" = 796 * 4.186 * 10^6 "erg/g"# , or#"6.02 kJ/mol"# . - The specific volume of a substance just an old way to specify a reciprocal density. Not that it matters, because we know that the densities should be close to
#"1 g/cm"^3# ... and they are:
#rho_w = 1/1.0001 "g/cm"^3 = "0.9999 g/cm"^3#
#rho_"ice" = 1/1.0908 "g/cm"^3 = "0.9168 g/cm"^3#
Now, since you have to examine the change in melting point with pressure variance, consider the Clapeyron equation:
#(dP)/(dT) = (DeltabarH_"fus")/(T_fDeltabarV_"fus")# where:
#(dP)/(dT)# is the slope of the two-phase coexistence curve on a phase diagram.#DeltabarH_"fus"# is the change in molar enthalpy of fusion in#"kJ/mol"# .#T_f# is the freezing point of the substance in#"K"# .#DeltabarV_"fus" = barV_w - barV_"ice"# is the change in molar volume in#"L/mol"# due to melting ice.
We already converted
#barV_w = [(0.9999 cancel("g H"_2"O"))/cancel("cm"^3) xx cancel("1 cm"^3)/cancel"mL" xx (1000 cancel"mL")/"L" xx ("1 mol")/(18.015 cancel("g H"_2"O"))]^(-1)#
#= 1/("55.504 mol/L") = "0.01802 L/mol"#
#barV_"ice" = [(0.9168 cancel("g H"_2"O"))/cancel("cm"^3) xx cancel("1 cm"^3)/cancel"mL" xx (1000 cancel"mL")/"L" xx ("1 mol")/(18.015 cancel("g H"_2"O"))]^(-1)#
#= 1/("50.891 mol/L") = "0.01965 L/mol"#
Now, to calculate the change in melting point, we consider the slope given by
In some small interval where the temperature and pressure change, we consider the reference temperature and pressure to be
#(dP)/(dT_f) ~~ (DeltaP)/(DeltaT_f) = ("3 atm" - "1 atm")/(T_f' - "273.15 K")#
The right-hand side of the equation becomes:
#(DeltaP)/(DeltaT_f) ~~ (6.02 cancel"kJ""/"cancel"mol")/("273.15 K" cdot (0.01802 cancel"L""/"cancel"mol" - 0.01965 cancel"L""/"cancel"mol")) xx (0.082057 cancel"L"cdot"atm")/(8.314472 xx 10^(-3) cancel"kJ")#
#= -"133.44 atm/K"# where we multiplied by a ratio of universal gas constants to ensure the units worked out.
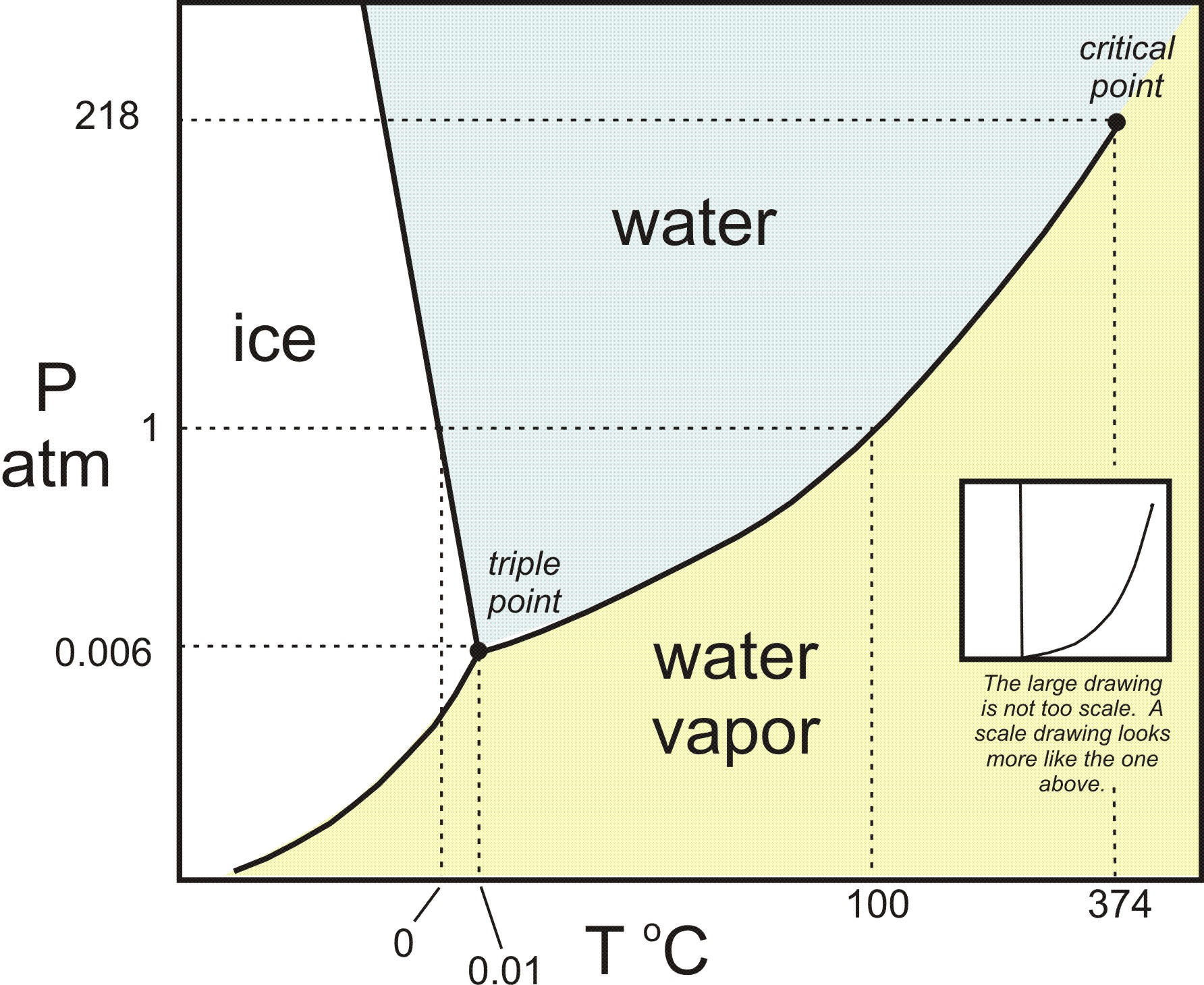
And if you look on the water phase diagram, this slope SHOULD be negative. This is because it requires INPUT of heat to melt (i.e.
As a result, the left-hand side becomes:
#("2 atm")/(T_f' - "273.15 K") = -"133.44 atm/K"#
Solve for the new freezing point to get that:
#T_f' = "2 atm"/(-"133.44 atm/K") + "273.15 K"#
#=# #ul"273.14 K"#
Or