Assuming #t = 4.5# means #"4.5 rad"#, I get #77.8^@# counterclockwise from negative x axis.
Well, assuming #t = 4.5# means #"4.5 rad"#, we know that there are #pi# radians for every #180^@#, so:
#4.5 cancel"rad" xx (180^@)/(pi cancel" rad") = 257.8^@#
The reference angle, though, is the smallest angle you can make from the #x# axis. So, we need this angle to be less than #180^@#.
If we start from the positive #x# axis (bisecting quadrants I and IV), then we are currently in quadrant III (bottom-left). Since quadrant III starts at #180^@# counterclockwise from the positive #x# axis, our reference angle is:
#257.8^@ - 180^@ = color(blue)(77.8^@)# counterclockwise from negative x axis
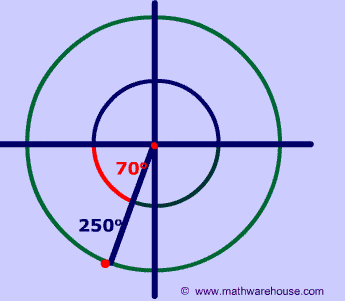
Another example is if the given angle was #250^@#. Then the reference angle would be #70^@# counterclockwise from the negative #x# axis: