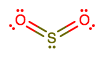
How do I correspond the structure of #"SO"_2# to a molecular orbital diagram?

#"SO"_2# is a bent structure (molecular geometry).

Sulfur wants #6# electrons, and so does oxygen. Hence, #6xx3 = 18# valence electrons to distribute throughout the structure.

• Putting #4# for each of two double bonds uses up #8#.
• You can then put #4# electrons on each oxygen and the last #2# on the sulfur as a lone pair. Sulfur can be hypervalent (cf. #"SF"_6#), but oxygen cannot because sulfur can access its #3d# orbitals (it's on the third period/row).

If we place this structure on the xy-plane, then the z-axis comes out towards us.

Sulfur has one #3s#, three #3p#, and five #3d# valence atomic orbitals (AOs), while oxygen has one #2s# and three #2p# valence AOs.

#\mathbf("SO"_2)# MO DIAGRAM

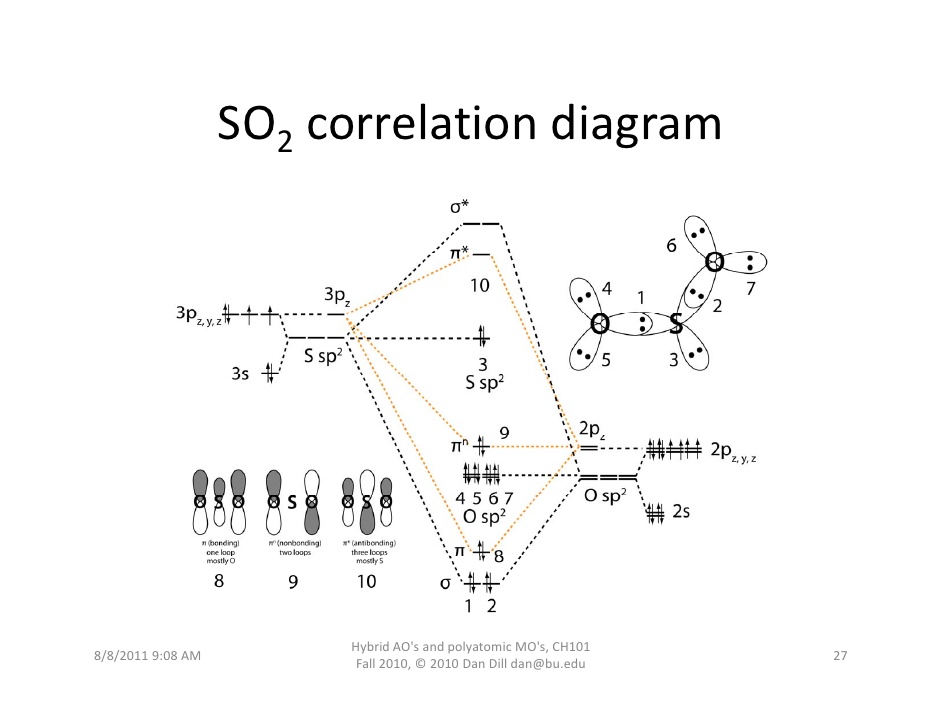
If you stare for a while at this diagram, which shows only the #sigma# bonds and lone pairs on the depicted structure...

SIGMA BONDING/ANTIBONDING ORBITALS

• The #2s# and #2p# orbitals on oxygen mix to produce hybridized #sp^2# AOs for #sigma# bonding (the hybridized orbitals are indicated by the "#"O"# #sp^2#" label on the far right of the diagram) that are intermediate in energy between the original #2s# and #2p# AOs.
• The #3s# and #3p# orbitals on sulfur mix to produce hybridized #sp^2# AOs for #sigma# bonding (the hybridized orbitals are indicated by the "#"S"# #sp^2#" label on the far left of the diagram) that are intermediate in energy between the original #3s# and #3p# AOs.
• Two of the #sp^2# AOs (#2s + 2p_x + 2p_y#) from oxygen can overlap head-on with two of the #sp^2# AOs (#2s + 2p_x + 2p_y#) from sulfur to form one #sigma# bonding and one #sigma^"*"# antibonding MO.
• The #sigma# bonding MOs are labeled 1 for the left #"S"-"O"# #sigma# bond, and 2 for the right #"S"-"O"# #sigma# bond. The antibonding MOs are empty.

As a result, we should see that we have accounted for the #sigma# bonding of the sulfur with each oxygen.

So far, our electron count is 2 x 2 = 4.

LONE PAIRS OF ELECTRONS (NONBONDING ORBITALS)

For the lone pairs of electrons, we examine the nonbonding MOs that have a dashed line connected to one atom's AOs but not the other's AOs. From the structure above, we should examine the diagonal orbitals, which have mixed #x# and #y# directions together, indicating a mixture of the #2p_x# and #2p_y# orbitals.

• One of sulfur's #sp^2# hybrid AOs aren't overlapping with one of oxygen's #sp^2# AOs. That is the lone pair of electrons that sulfur has, and you can tell by noticing how the MO diagram shows the black dashed-line contribution from only the #sp^2# AOs of sulfur.
• This is orbital 3 and is labeled as the nonbonding "#"S"# #sp^2#" MO in the middle of the diagram, below MO 10.
• There are #sp^2# orbitals of oxygen that didn't overlap with the #sp^2# orbitals of sulfur. Those account for the two lone pairs of electrons on each oxygen, and you can tell by noticing how the MO diagram shows the black dashed-line contribution from only the #sp^2# AOs of oxygen.
• These are MOs 4, 5, 6, and 7, labeled "#"O"# #sp^2#", and they are right below MO 9.

So far, our electron count is (2 x 2) + 2 + (2 x 4) = 14.

PI BONDING/ANTIBONDING/NONBONDING ORBITALS

Lastly, let us examine the #\mathbf(pi)# bonds. The additional #pi# bond on top of each sulfur-oxygen #sigma# bond requires two more electrons per #"S"-"O"# connection.

• The gist is that two #\mathbf(pi)# bonds are made between the #2p_z# AOs of each oxygen and the #3p_z# of the sulfur. That makes sense since we had defined the axis coming towards us as the z-axis, the #2p_z# and #3p_z# orbitals both lie along that axis, and we hadn't considered those orbitals yet. They can overlap side-on to form #pi# bonds.

(I believe they are labeled as MOs 8 and 9 on the MO diagram, but I am unsure why 9 is nonbonding when in fact four #pi# electrons are needed. Perhaps it has something to do with the #3d# orbital access, but that is just speculation.)

And our final, total electron count is (2 x 2) + 2 + (2 x 4) + (2 x 2) = 18, as predicted in the beginning.