How do you solve for the energy difference between #n = 1# and #n = 2# in hydrogen atom?

2 Answers
Truong-Son N.
May 21, 2015

The difference in energy is solved for with the Schrodinger equation, exactly.

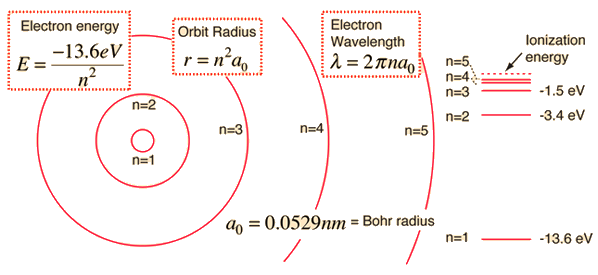
The actual expression is more complicated than we care about, but the energy levels for the Hydrogen atom from the first quantized energy level to the next in terms of atomic units simplifies it a lot, and is given by:

#E_n = -"13.6058 eV" cdot Z^2/n^2#

where #Z = 1# for hydrogen atom and #n# is the principal quantum number.

Hence, we take the difference (again, with #Z = 1#) to get what is known as the Rydberg Equation:

#DeltaE_(n_i->n_f) = -"13.6058 eV" cdot (1/n_f^2 - 1/n_i^2)#

So,

#color(blue)(DeltaE_(1->2)) = -"13.6058 eV" cdot (1/2^2 - 1/1^2)#

#=# #color(blue)"10.2044 eV"#

Michael
May 21, 2015

The difference is 10.2eV

You can work out the difference using the expression:

#E=-(13.6"eV")/(n^2)#

Where #n# is the principle quantum number.

#E# is the energy in electron volts. ( 1eV = #1.6xx10^(-19)"J"#)

hyperphysics.phy-astr.gsu.edu
(From Hyperphysics.edu)

So the difference between #n=1# and #n=2# is:

#(-13.6)/(1^2)-((-13.6))/(2^2)#

#=-13.6+13.6/4#

#=-13.6+3.4#

#=-10.2"eV"#

Related questions
Impact of this question
3013 views around the world
You can reuse this answer
Creative Commons License