Question #f8f28

It depends on what you mean.

Molecular motion can be split into translational, rotational, and vibrational motion.

• Translational motion is simply forward, linear movement.
• Rotational motion is, of course, based on rotating the molecule in space around arbitrary axes (usually #x#, #y#, and/or #z#).
• Vibrational motion is the inward and outward motion of atoms on a molecule in specific ways: symmetric/asymmetric stretches or symmetric/asymmetric bends.

TRANSLATIONAL MOTION

Given the tenets of Collision Theory, molecules have to collide effectively for a reaction to occur. Naturally, if molecules could not move around translationally, it would be impossible for collisions, and thus reactions, to occur.

Since reactions occur, translational motion exists for all molecules at #T > "0 K"#. Reactions occurring are evidence in themselves.

ROTATIONAL-VIBRATIONAL MOTION

Vibrational motion is generally based off of the harmonic oscillator model, where two atoms are connected by a stiff spring that compresses and stretches. With these motions there exists a vibrational quantum number #upsilon = 0, 1, . . . , n# corresponding to vibrational energy levels.

Rotational motion is generally based off of the rigid rotor model, where two atoms are connected by a stiff rod and the rotation axis bisects the two atoms. With these motions there exists a rotational quantum number #J = 0, 1, . . . , n# corresponding to rotational energy levels.

Both types of motion can be detected via rotational-vibrational spectroscopy, such as IR, Raman, and microwave spectroscopy.

Rotational and vibrational motions, together, yield the following ro-vibrational model that incorporates centrifugal distortion (the coupling of rotational with vibrational motion):

One example of recorded ro-vibrational motion is in the allowed transitions for #upsilon = 0# from the ro-vibrational IR spectrum of gaseous #"HCl"#, which I took myself in 2015:

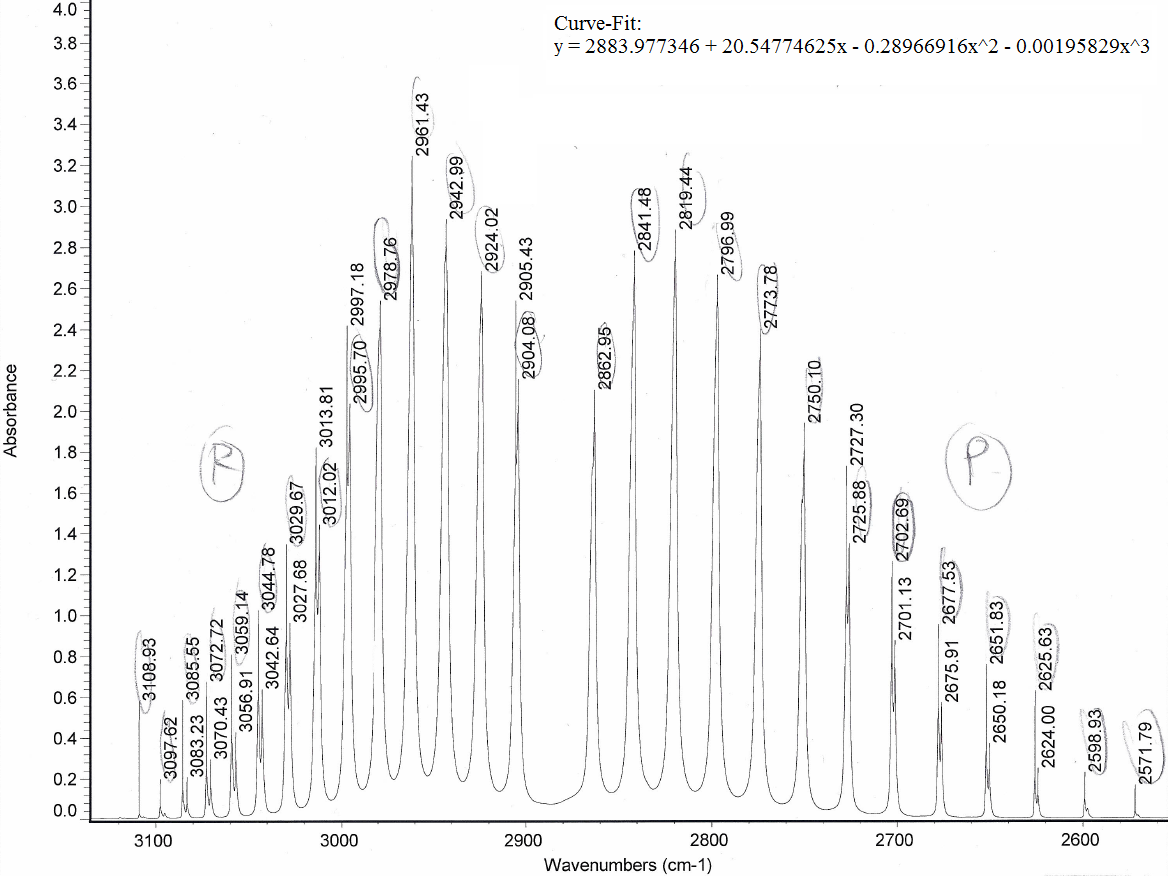
The shown window of this spectrum corresponds to the allowed fundamental ro-vibrational transitions of #"HCl"#, for vibrational energy level #upsilon = 0#.

The #P# and #R# branches are the sets of peaks corresponding to rotational motion.

The equation on there was:

#\mathbf(tildenu(m) = tildenu_0 + (2tildeB_e - 2tildealpha_e)m - tildealpha_em^2 - 4tildeD_em^3)#

where:

• #tildenu_(upsilon)(m)# is the frequency in #"cm"^(-1)# for a particular vibrational energy level #upsilon#, corresponding to ideal vibrational motion.
• #tildenu_0# is the fundamental frequency found in the #Q# branch, which is the "hole" in between the #P# and #R# branches at #"2883.97 cm"^(-1)#. Here, vibrational energy level #upsilon = 0#.
• #m# is the slope when the circled frequencies are used as values on the horizontal axis of a graph of #tildenu(m)# vs. #m#.
• #tildeB_e# is the equilibrium rotational constant, which corresponds to ideal rotational motion.
• #tildealpha_e# is the equilibrium ro-vibrational coupling constant, corresponding to the deviation away from ideal vibrational motion due to coupling with rotational motion.
• #tildeD_e# is the equilibrium centrifugal distortion constant, corresponding to the deviation away from ideal rotational motion due to coupling with vibrational motion.

The distances between each peak, as seen in the diagram below, are approximately equal to #2tildeB_e#:

You can see in the above diagram that the rotational energy levels #J# are more closely spaced than the vibrational energy levels #upsilon#.

Thus, the rotational energy levels form the fine-structure in the above ro-vibrational IR spectrum, i.e. the individual peaks within each branch #P# and #R#.